Sinuskurve

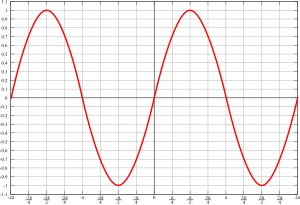
Sinuskurva, eller sinusoiden er forma til den grafiske framstillinga av dei to trigonometriske funksjonane sin(x) og cos(x), som begge er projeksjonen av rørsla til eit punkt langs ein sirkel.

Cosinusfunksjonen. Denne er òg ein sinusoide.

Eigenskapar

Ei sinuskurve er fullt skildra av to storleikar: avstanden mellom to toppar i x-retninga (kalla perioden) og avstanden frå midtlinja til maksimal- eller minimalverdien i y-retning (kalla amplituden).

Sinuskurva er spesielt viktig for å skildre mekaniske og elektroniske rørslefenomen, det vil seie når x skildrast som tid. Då er avstanden mellom to toppar lik periodetida og er den inverse av frekvensen. t = 1/f.

Den deriverte av ei sinuskurve skildrar stigninga til kurva, og den deriverte er òg ei sinuskurve.

Det er denne derivasjonseigenskapen som gjer at sinuskurva finst overalt innan elektronikk. Ingen andre kurveformer kjem uforandra gjennom kva for eit som helst nettverk av motstandar, spolar og kondensatorar. Amplituden blir vanlegvis ikkje uendra.

Masse-fjørsystem i rørsle‎

Sinuskurva kjem òg ut av differensiallikningane for enkle oscillatorar med resonanseigenskap, som masse fjører og spole-kondensator-system.

For praktiske utrekningar er det svært viktig at den deriverte av ei sinuskurve blir ei cosinuskurve som har same amplitude som sinuskurva. Dette lettar reknearbeidet mykje sidan faktoren blir lik 1 ved operasjonen. Ved ein særskild samanheng mellom x og frekvensmålet vil dette inntreffe: x = ω*t, der ω = 2*π*f. Dette kjem av at perioden til sin(x) har lengda 2*π i rein matematikk. Vinkelmålet 360°/(2*π) = 57.2958° har fått namnet radian og frekvensen ω blir målt i radianar per sekund. f er gjeven i Hz, svingingar (periodar) per sekund.

Sjå òg

Kjelder

Denne artikkelen bygger på «Sinuskurve» frå Wikipedia på bokmål, den 14. februar 2012.